La Tabla de verdad de la disyunción

Veamos ahora la construcción de la tabla de verdad de la disyunción.

Pongamos como ejemplo la proposición compuesta:

“Luis es inteligente o simpático”.

Paso 1

Determino cuántas proposiciones simples tengo:

Observo que tengo dos:

1. “Luis es inteligente”
2. “Luis es simpático”

Recordemos que por cuestiones de estilo no repito el sujeto, pero sé que me refiero al mismo sujeto (Luis, en este caso) en ambas oraciones.

Paso 2

Sustituyo cada proposición con una letra:

p: “Luis es inteligente”

q: “Luis es simpático”

Paso 3

Simbolizo la proposición:

p ∨ q

Paso 4

Para poder dibujar una tabla en la que quedarán escritas las proposiciones en la parte superior y los valores de verdad que asumen las mismas justo debajo de ellas, se necesita aplicar la siguiente fórmula para saber cuántas posibles combinaciones de verdad tiene mi proposición compuesta:

2ⁿ

Donde 2 se refiere a los valores de verdad que puede asumir una proposición (que dentro de esta Lógica sólo son dos: verdadero o falso) y “n” se refiere al número de proposiciones simples que conforman la proposición de la que queremos construir la tabla.

En el ejemplo tenemos:

2ⁿ

Donde 2 significa los valores de verdad: verdadero y falso y 2 el número de proposiciones simples.

Realizo la operación que me da como resultado 4:

2² = 2 x 2 = 4

Con ello sé que mi tabla tendrá cuatro filas o renglones.

Ahora puedo dibujar la tabla:

Para asignar los valores de verdad de las proposiciones simples escribo los valores de derecha a izquierda y anoto una V (de verdadero) y una F (de falso). En la siguiente columna duplico el número de verdades y de falsedades. Si hubiera una tercera proposición simple sigo duplicando, es decir, tendría cuatro verdades y cuatro falsedades y así sucesivamente.

Con esta operación obtengo:

Paso 5

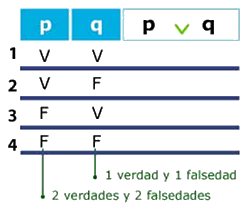
Realiza la tabla de la proposición compuesta p ∨ q.

Existen dos tipos de disyunciones: la inclusiva y la exclusiva, aquí sólo nos ocuparemos de la primera, así cuando hablemos de disyunción siempre nos estaremos refiriendo sólo a ella.

El único caso de falsedad de una disyunción es cuando ambas proposiciones son falsas. Cualquier otra combinación de valores de verdad entre las proposiciones que conforman la proposición compuesta es verdadera.

A diferencia de la conjunción, la disyunción es como un sistema eléctrico en paralelo. Cuando hay una conexión eléctrica en paralelo, una de las lámparas puede no funcionar pero el sistema, la disyunción, continúa funcionando.

De esta forma tenemos que basta con que Luis tenga alguna de las dos características  para que toda la proposición compuesta sea verdadera, no se requiere que posea las dos forzosamente como en la conjunción:

• Si Luis posee las dos características, es decir, es inteligente y simpático, entonces la proposición compuesta es verdadera.
• Si Luis es simpático, pero no es inteligente, de cualquier forma la proposición compuesta es verdadera.
• Si resulta que Luis no es ni inteligente pero sí es simpático, la proposición compuesta sigue siendo  verdadera.
• Pero si Luis no posee ninguna de las características, es decir, no es simpático ni inteligente, entonces la proposición compuesta es falsa.

De esta forma tenemos la siguiente tabla:

Tenemos, pues, que para ser verdadera la proposición compuesta, cuya conectiva lógica principal es una disyunción, basta con que alguna de las proposiciones simples que la componen sea verdadera y el único caso de falsedad es cuando ambas proposiciones simples son falsas.

Autoevaluación

Tablas e infografías

Descarga el siguiente documento dando clic aquí para poder realizar la actividad.

descriptionDocumento

1. Con base en la información que se te proporciona en la infografía redacta cinco enunciados por lo menos con tres conectivos lógicos, simbolízalos y construye una tabla de verdad con ellos.
2. Para construir de manera adecuada la tabla de verdad sigue los cinco pasos que acabas de estudiar.
3. Analiza los resultados de la tabla y los porcentajes que se muestran en la infografía y redacta una conclusión que puedes inferir a partir de dicha información.
4. Después realiza tu evaluación con la Rúbrica de cotejo “Tablas e infografía”.

descriptionDocumento